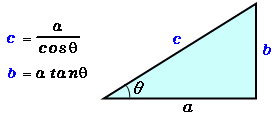
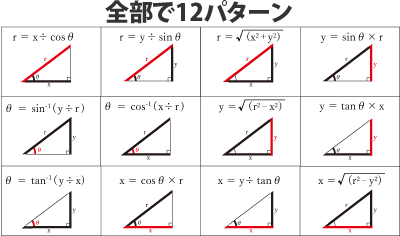
高校で習う三角関数ですが、当然数学検定でも前提知識として求められます。 三角関数の基本となる、 sin 、 cos 、 tan に関しては求め方と意味をまずは理解しましょう。 そうする事で後々出てくる公式の意味や求め方もスムーズに理解出来るようになります。三角関数の具体的な使い方 正弦 (sin)・余弦 (cos)を使うことで斜辺の長さとその角度から幅と高さを得ることができます。 この計算式は地形の測量・ベクトルの座標計算・ゲームキャラクターの移動など様々な場面で活用できます。 x = cosΘ × h y = sinΘ × h三角関数は周期関数なので、逆関数は多価関数である。 逆関数の性質から以下が成り立つ: =,() = / /ピタゴラスの定理 ピタゴラスの定理やオイラーの公式などから以下の基本的な関係が導ける 。 = ここで sin 2 θ は (sin(θ)) 2 を意味する。 この式を変形して、以下の式が導かれる:

余弦定理で角度を求める方法 数学の星
三角形 角度 求め方 sin
三角形 角度 求め方 sin-特に,相似な三角形の面積比は相似比の二乗に比例することも分かります。 →相似比と面積比,体積比の公式の証明 また,サインの性質: sin θ = sin (18 0 ∘ − θ) \sin \theta=\sin (180^{\circ}\theta) sin θ = sin (18 0 ∘ − θ) に注意すると,円に内接する四角形 三角比は、xy平面の力を借りて、基準となる角度が 90° 以上の場合でも考えていくことができる。 三角比では0°から180°の角を、そして「三角関数」では180°より大きい角などに広




タンジェントとは何か 中学生でも分かる三角関数の基礎
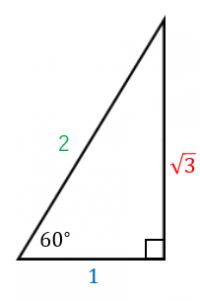
3 正四角錐の側面は『二等辺三角形』 三角錐の側面は『三角形』 三角錐の時も側面は二等辺三角形じゃないん ;答え 二等辺三角形が2つくっついている問題ですね。 この場合、それぞれの二等辺三角形に注目して角度を1つずつ求めていきます。 赤い二等辺三角形は、頂角が36°なので 底角1つ分の角は となります。 そこから、次は青い二等辺三角形に注目して を直角三角形の左端の角度が30度の時のそれぞれの辺の長さの比を覚えていますか? 三角形の比についてよくわからない方は、三角比(30°,45°,60°) をみてください。 それでは、sin30°、cos30°、tan30°の求め方を説明していきます。 sin30°の求め方 上の直角
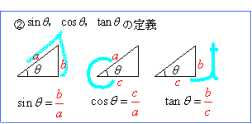
サインから角度を計算する方法 asin関数 を使用すると、サインから角度を計算することができます。 サインは、直角三角形の斜辺に対する対辺の比のことで、「対辺の長さ÷斜辺の長さ」になります。・15度や18度などの三角比も計算することができますが、30度や45度よりかなり大変です。 関連:sin15度、cos15度、tan15度の値と求め方 関連:cos72度、sin18度の2通りの求め方 次回は 単位円を使った三角比の定義と有名角の値(0°~180°) を解説します。解説 ≪三角比の値の求め方≫ sinθ,cosθ,tanθの値は,次の「よく出る2つの三角形」と「sinθ,cosθ,tanθの定義」を覚えていれば導けます。 これらを使った求め方 ①θの値(角度)を見て,「よく出る2つの三角形」のうち,当てはまる三角形をかき出す。
余弦定理を変形すれば、 b , c , a が分かっているときに A を求めるという使い方もできます: a 2 =b 2 c 2 −2bc cos A この式をよく見ると、 「右辺は辺の長さだけ」 でできており、 左辺は角度だけ でできています。 したがって、この式を利用すると 「3辺の三角比の値の覚え方と求め方 ここでは、三角比 \(\sin\), \(\cos\), \(\tan\) の値の覚え方と求め方について詳しく解説していきます。 ① 単位円を使いこなす はじめに、単位円を用いた三角比の値の求め方を理解しておきましょう。 36度の三角比 次の図は、 $\mathrm{ AB }=\mathrm{ AC }$ の二等辺三角形 ABC をかいたものです。 $\angle \mathrm{ A }=36^{\circ}$ で、 $\mathrm{ BC }=1$ とします。今、 $\mathrm{ AB }=x$ とおいて、これを求めてみましょう。これがわかると、36度の三角比も求められるようになり




三角関数の公式の一覧 Wikipedia




高校数学 直角三角形を用いた三角比 Sin8 Cos8 Tan8 の定義とその理由 30 45 60 の三角比 受験の月
三角形の角度を求める問題 ではこれらの性質を使って、三角形の角度を求める問題を解いていきたいと思います。 問題① 下の図における ∠x の大きさを求めなさい。 三角形の外角の大きさ=となり合わない2つの内角の和 であることから x+60°=135°エクセルで sin の値が になるθを この記事では、三角関数について、角度の求め方や変換公式(\\(90^\\circ − \\theta\\) など)について解説していきます。 計算問題もわかりやすく説明していくので、この記事を通してぜひマスターしてくださいね!



直角三角形ではない場合ピタゴラスの定理はどう使えるのでしょうか Quora



3分でわかる 三角関数の角度の求め方 三角方程式を解く 合格サプリ
三角関数 sin cos tan asin acos cos1 atan degrees radians の使い方 直角三角形は一カ所の角度が決まると、辺の長さの比率が決まります asin は指定の sin の値になる θ を求めます;三角形の証明・形状問題 → 携帯版は別頁 三角関数の合成公式 a sin θb cos θ の形の式は一つの三角関数にまとめることができます.これを三角関数の合成公式といいます. a sin θb cos θ= √a2b2√nnnnni sin (θα) (ただし, α は cos α= 1 三角形ABCの外接円の中心をO、半径をR三角形ABCの内接円の中心をI、半径をr AB=7BC=8 ;




三角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ




タンジェントとは何か 中学生でも分かる三角関数の基礎
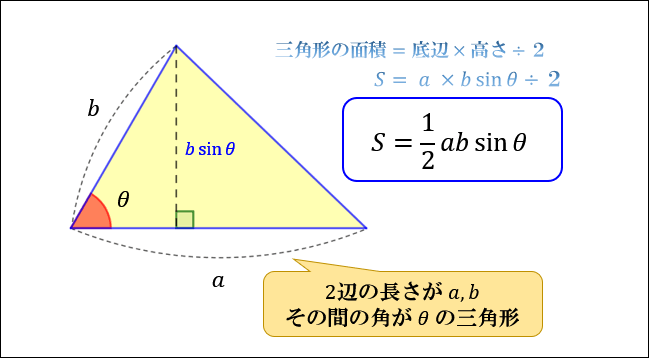
正弦定理から,三角形の辺の長さを求める計算について ABCにおいてa = 3 ,A = 60°,B = 45°のときbを求めよ。 という問題がありますが, これを定理にあてはめていって, b = 3 / sin60°× sin45° まではつくれるんですが,そこから (3 ÷ √3/2 ) × 1/√2= 6/√6=√6 というのになるのが,意味がわかりま直角三角形 110 /2件 表示件数 5 10 30 50 100 0 1 1245 60歳以上 / その他 / 非常に役に立った /「三角関数から三角形の面積が求められるの?」 そうなんです! 三角形の2辺とその間の角が分かれば、三角形の面積は求められるのです! 今回は三角形の面積をsin(サイン)を用いて求める公式をまとめましたので、ぜひ最後まで読んで見てください!




数学 三角比 Sin Cos Tanの公式まとめ 表 変換 相互関係 面積 正弦定理 余弦定理 理系ラボ




三角関数の基礎 角度の求め方とは Sin8 1 2から8を計算 高校生向け受験応援メディア 受験のミカタ
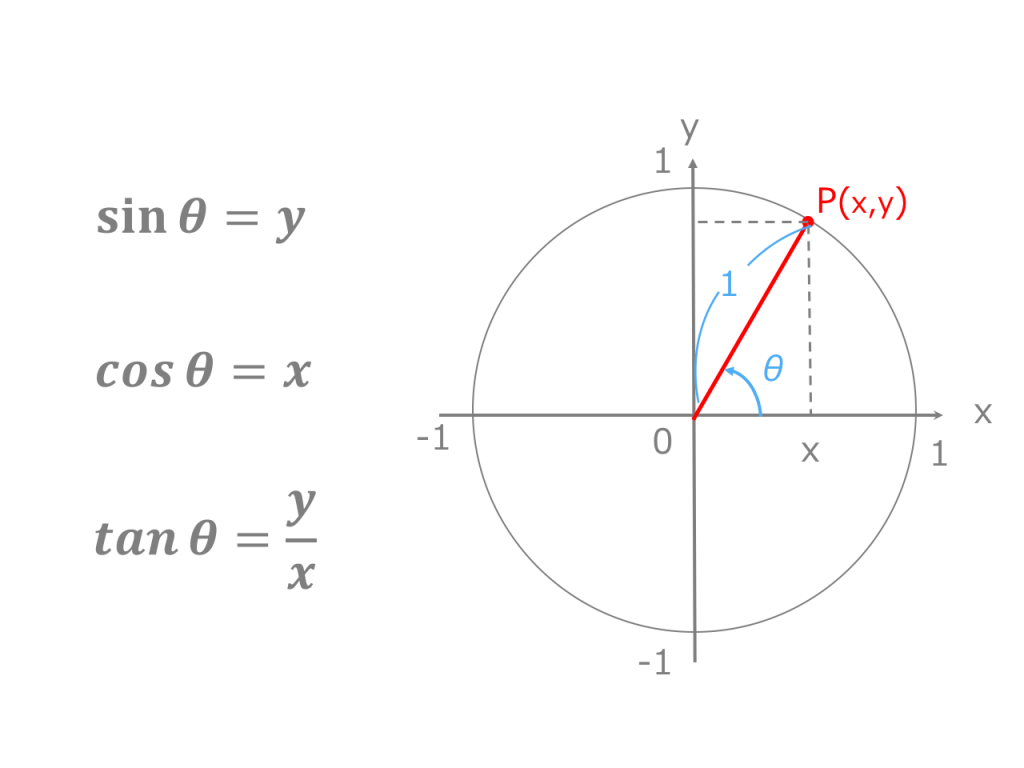
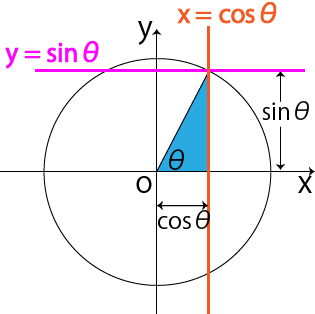
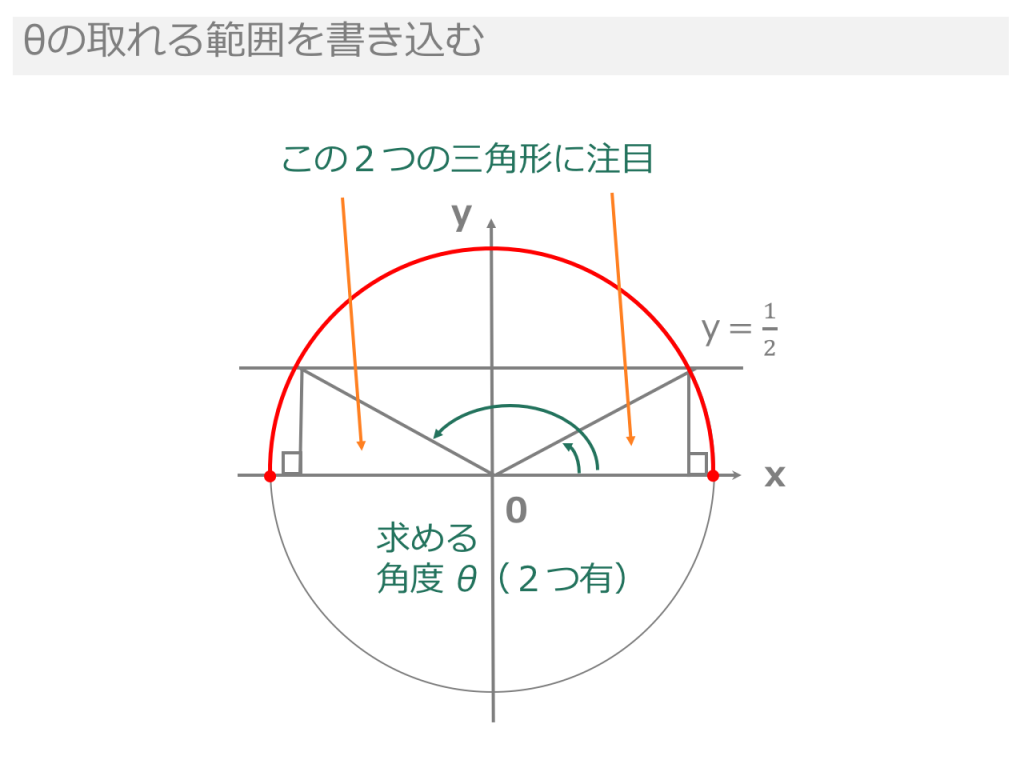
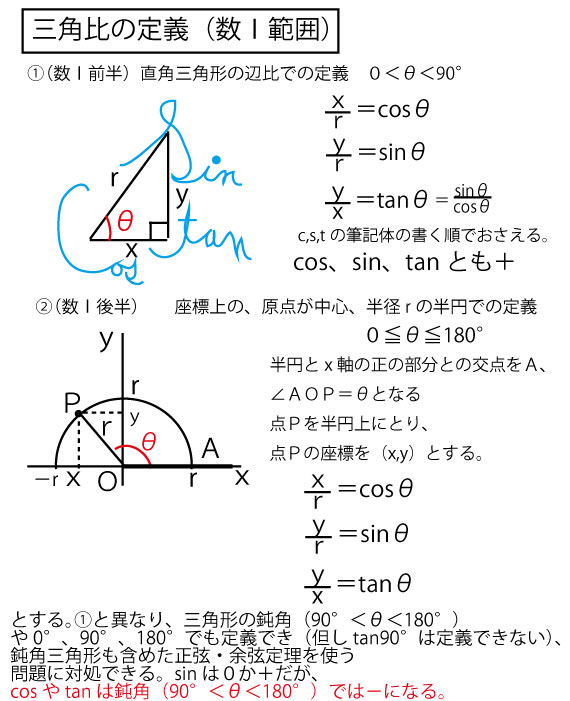
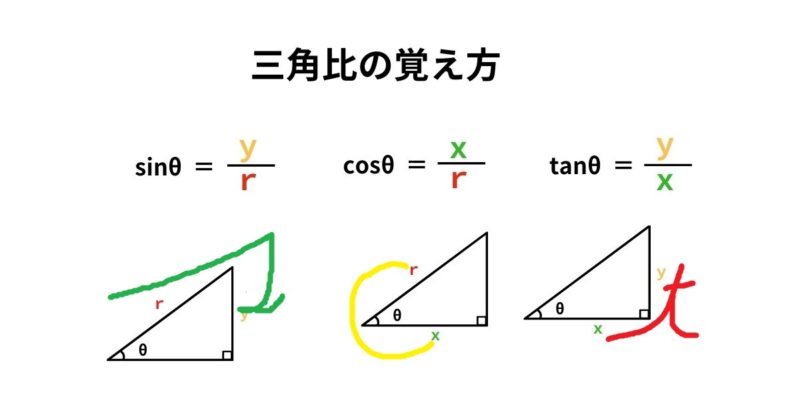
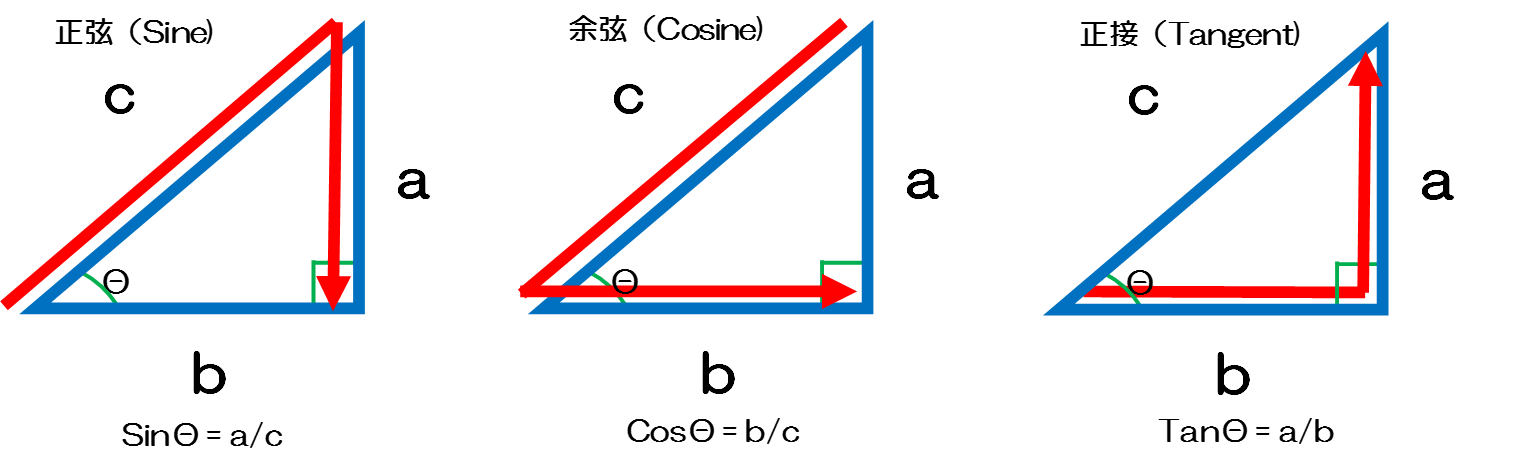
180°− θ と θ の三角比の関係は,公式として暗記するのではなく,上のような図をかいて求められるようにしておくのがよいですね。 では,これからも『進研ゼミ 高校講座』を活用して,得点を伸ばしていってくださいね。 その他にも苦手なところは< 鈍角の三角比1 > 角度θが90 以上の場合の三角比を 次で定める。 正の数r に対し,点Q(r,0) を原点 O(0,0) を中心として反時計まわりに角 度θだけ回転した点をP(X,Y) とする。 このとき角度θにおける三角比を sinθ= Y r, cosθ= X r, tanθ= Y X で定める。はじめに少し三角関数のおさらいをしておきましょう。 三角関数とはご存知のとおり ・正弦(サイン) ・余弦(コサイン) ・正接(タンジェント)etc のことですが、これは直角三角形の形が同じ(角度が同じ)であれば辺の長さが比例することから導き出された公式です。




黄金三角形による18 シリーズの三角比 おいしい数学




15 シリーズの三角比 おいしい数学
4 数学についての質問です ABCで sin²Asin²Bsin²C 「 x 軸の正の部分」と線分 OA による(反時計回りを正とする)角の大きさ ∠BOA = θ に対して sinθ = y r, cosθ = x r, tanθ = y x で表される3つの三角比の関数のことを、 三角関数 と言い三角形の「2辺の長さの比」が正弦の値になるのは直角三角形の場合だけで、それ以外の場合には sin A の値は「2辺の長さの比」にはなりません。 (右図イのような場合も含めて)一般に、角度 A の値によって sin A の値が決まり、これとは別に辺の長さが決められていると考えることが重要です。
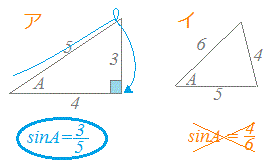



正弦定理



三角形とは 面積公式 角度 辺の長さ 重心 比の計算 受験辞典
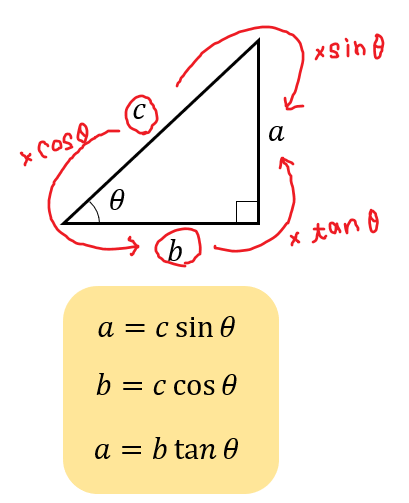
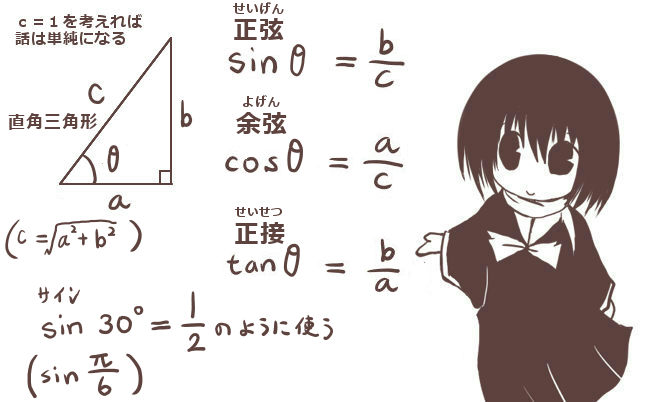
三角形の2辺の長さと直角ということを利用し、残りの角のひとつを出したいと考えています。 やり方として、三平方の定理で角度を出す、「COSθ=b/a」 (b,aは三角形の辺の長さです) を使用してやろうと考えております。 その角度θを今プログラム的に求め サイン(sin)、コサイン(cos)、タンジェント(tan)の計算をする前に、三角関数の基本をおさらいしておきましょう。 直角三角形の3辺 a、b、c は、以下のような関係にあります。 例えば、辺cの長さが5で、角度θが30°だった場合、辺aの長さは以下のようになります。 このページは、このような人へ向けた内容となっています 三角比を使った三角形の面積の求め方を知りたい 三角比の公式は知っているが使い方がわからない 三角形の面積を求めるための、色々な方法を知りたい 三角比(\\(\\sin, \\cos, \\tan\\))を使った三角形の面積を求める方法はいく




三角関数で角度から座標を導くふたつの式の使い途 Qiita



三角関数の基礎 角度の求め方とは Sin8 1 2から8を計算 高校生向け受験応援メディア 受験のミカタ
図形と計量sin,cos,tanの値の覚え方 図形と計量tanの値からcosの値を求めるときの分数の式変形について 図形と計量「なす角」の意味 図形と計量三角形における三角比の値 図形と計量三角形の3辺が与えられたときの面積の求め方52°の三角形の辺の比はわかりませんが,sin 52°,cos 52° の値なら計算機に打ち込めばすぐ求められます。 もちろん52°というのは1つの例であって,他のどんな角度でも sin,cosを斜め方向の力に かけ算することで分力を求めることが可能 です。Sin θ ,cosθ ,tanθ 図形と計量cosの値が負になるときの角度の求め方 図形と計量sinを含む分数の式の計算方法 図形と計量三角形の3辺が与えられたときの面積の求め方 図形と計量三角形の辺の長さを求めるときの三角比の値




高校数学 三角比 三角比を使った三角形の面積の求め方 Sin Cos ヘロンの公式を使った方法 数学の面白いこと 役に立つことをまとめたサイト



三角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ
三角形の各辺や角度を調べる時です。 sin / cos / tan 理数系じゃないので苦手なんですよね。 傾斜の求め方がよくわかった。 30°,60°の求め方 正三角形を2つにわけた図形をイメージします。この三角形は30°,60°,90°の三角形で辺の長さの比が12\( \sqrt{3} \)です。これを使って三角比で求めます。 45°の求め方 直角二等辺三角形をイメージします。三角関数から角度 (逆三角関数) ツイート 三角形の計算 ・ 正三角形 (辺から高さと面積) ・ 正三角形 (高さから辺と面積) ・ 正三角形 (面積から辺と高さ) ・ 直角三角形 (底辺と高さ) ・ 直角三角形 (底辺と



三角関数の角度の求め方や変換公式 計算問題も徹底解説 受験辞典



Sin Cos Tanの値の覚え方 数学 苦手解決q A 進研ゼミ高校講座




高校数学 三角比 三角比を使った三角形の面積の求め方 Sin Cos ヘロンの公式を使った方法 数学の面白いこと 役に立つことをまとめたサイト



3




型枠大工の為の計算方法 関数計算 Sin Cos Tan 池坊徳夫のブログ 型枠計算法




高校数学 三角比 三角比を使った三角形の面積の求め方 Sin Cos ヘロンの公式を使った方法 数学の面白いこと 役に立つことをまとめたサイト




三角形の辺から角度を計算 製品設計知識




直角三角形ではない時 Sinの値を求める場合 円周角の定理から角度が8の時の直角三角 Clear




わかりやすい三角比と基本公式 Irohabook




高校数学 直角三角形を用いた三角比 Sin8 Cos8 Tan8 の定義とその理由 30 45 60 の三角比 受験の月




タンジェントとは何か 中学生でも分かる三角関数の基礎



3分でわかる 三角関数の角度の求め方 三角方程式を解く 合格サプリ



高1数学 木の高さを三角比を用いて求める方法を解説 数スタ



三角関数をマスターしよう その3 金属加工 ものづくり初心者のメモ帳 Mc マシニングセンター Ncプログラムの学習



三角関数 1 Cg 数学 06aa



三角関数の角度は 3分でわかる求め方 公式と計算 表との関係




三角形の辺や角が与えられたとき残りの辺や角を求める方法 数学の偏差値を上げて合格を目指す



C言語入門 三角形の2辺とその間の角度から面積を計算 Webkaru



直角三角形の角度の求め方 教えて下さい 斜辺以外の2辺の長さが分かっ Yahoo 知恵袋




15 75 105 165 の三角比 数学i フリー教材開発コミュニティ Ftext
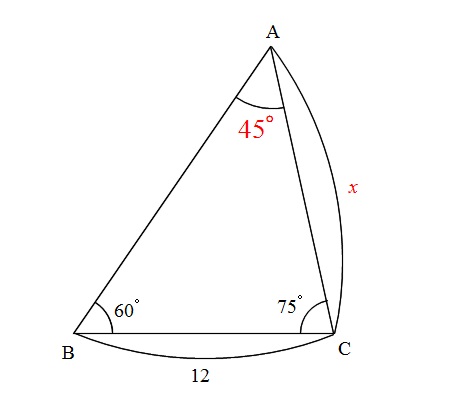



三角形で角度が2つ分かっているのに正弦定理も余弦定理も使えない
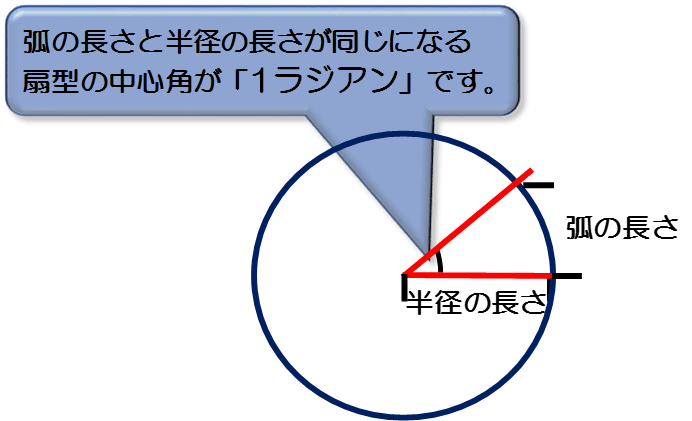



Vba 三角比をもとめる Sin関数 Cos関数 Tan関数 角度をもとめる Atn関数



数i 基本的な三角比の値




三角関数の基礎知識




図形の調べ方 三角形 役に立つ角度の求め方 苦手な数学を簡単に
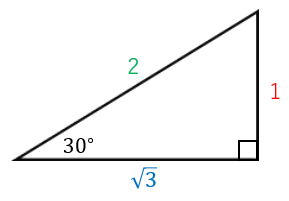



30度 45度 60度のsin Cos Tan 具体例で学ぶ数学




三角関数の知識 やさしい電気回路




三角形の面積の求め方とは Sinやベクトルを用いる公式も解説 小学生から高校生まで 遊ぶ数学




Sin Cos Tan 三角比 三角関数の基礎をスタサプ講師がわかりやすく解説 高校生なう スタディサプリ進路 高校生に関するニュースを配信
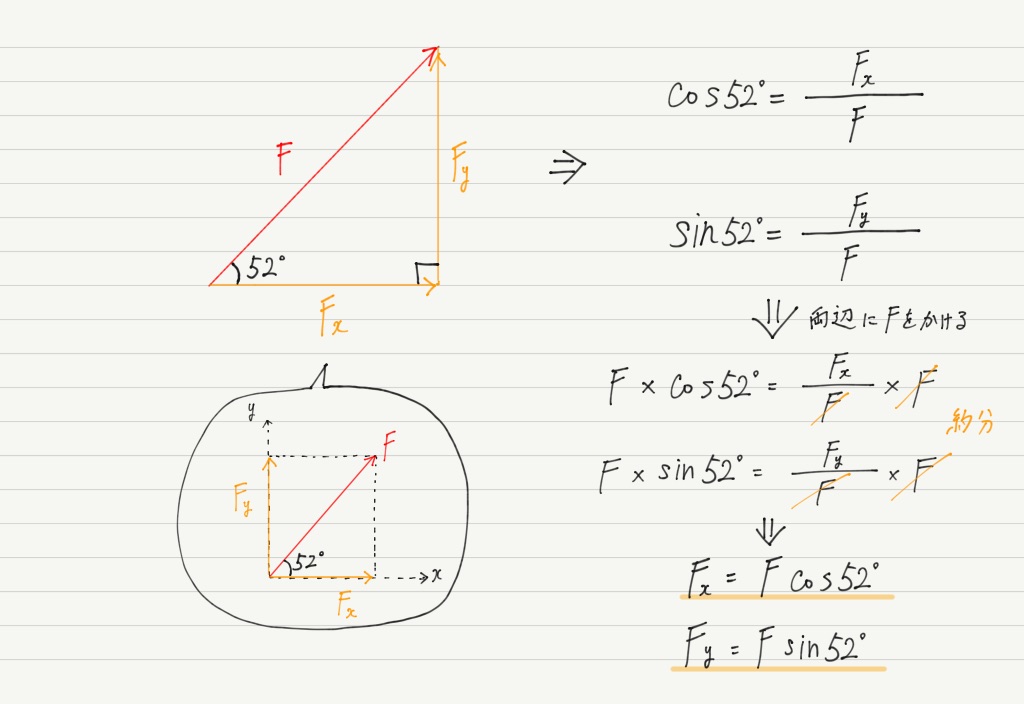



力の分解 三角比編 高校物理をあきらめる前に 高校物理をあきらめる前に




サイン コサイン タンジェントの角度の求め方 一歩一歩ぐんぐんブログ



21年大学入試共通テスト 数学ia 第1問 2 図形 三角比 余弦定理 正弦定理など 配点点 問題 解答 解説 船橋市議会議員 朝倉幹晴公式サイト
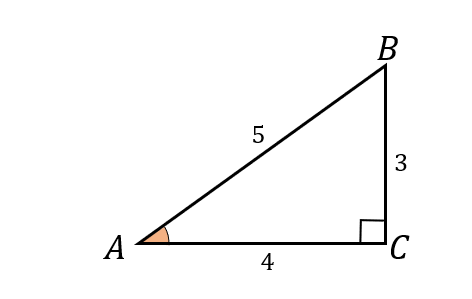



三角比の値の求め方 数学苦手な人に向けて基本をイチから解説していくぞ 数スタ




三角形の面積




タンジェントとは何か 中学生でも分かる三角関数の基礎
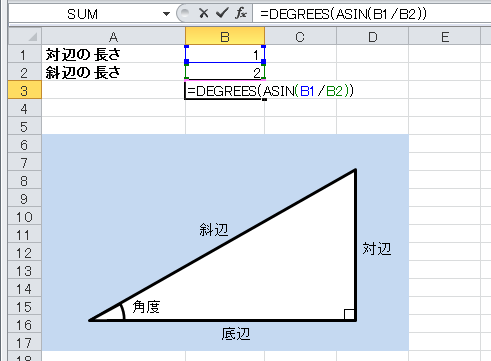



サインから角度を計算するには Asin Degreesの解説 エクセル関数リファレンス
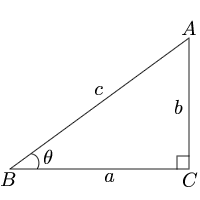



三角関数から角度 逆三角関数 三角形の計算 計算サイト




高校数学 三角比の入り口 Sin Cos Tanとは 数樂管理人のブログ



直角三角形の斜辺の長さと角度が分かっている場合 他の2辺の長さを求めたいので Yahoo 知恵袋




サイン Sin を使って三角形の面積を求める練習問題一覧 数学i By ふぇるまー マナペディア



三角関数 機械加工でよく使う計算方法を説明します セドヤのブログ




高校数学 三角比 三角比を使った三角形の面積の求め方 Sin Cos ヘロンの公式を使った方法 数学の面白いこと 役に立つことをまとめたサイト




有名角 準有名角のsin Cosの値 一覧 理系のための備忘録



直角三角形の辺の比の関係 Sin Cos Tan 理数系無料オンライン学習 Kori




三角形の3辺から角度を計算 高精度計算サイト




底辺と高さから角度と斜辺を計算 高精度計算サイト



角度と底辺から斜辺と高さを計算 高精度計算サイト




三角関数は何に使えるのか サイン コサイン タンジェントの活躍 Qiita



三角関数について




Javaでmathクラスを使って三角関数を求める方法を現役エンジニアが解説 初心者向け Techacademyマガジン




余弦定理で角度を求める方法 数学の星



三角比の表と面積公式 正弦定理 余弦定理を一記事で解説



3



30度 45度 60度のsin Cos Tan 具体例で学ぶ数学




底辺と角度から 高さを求める ある高さの木から 10m離れて 木のてっ Okwave



1




高校数学 数 76 三角比 基本編 Youtube




高校数学 三角比 三角比の求め方と覚え方 Sin Cos Tan 数学の面白いこと 役に立つことをまとめたサイト




三角関数 機械加工でよく使う計算方法を説明します セドヤのブログ




サインコサインタンジェント Sin Cos Tan とは何を表す 良い覚え方を紹介 遊ぶ数学




わかりやすい三角比と基本公式 Irohabook



直角三角形の解法 1



三角関数をマスターしよう その2 金属加工 ものづくり初心者のメモ帳 Mc マシニングセンター Ncプログラムの学習




三角比を用いた計算問題をマスターしよう スタディクラブ情報局




関数電卓の使い方 三角関数 Itよろず雑記帳



2 4 三角関数の微分



Vba 三角比をもとめる Sin関数 Cos関数 Tan関数 角度をもとめる Atn関数



Sinを用いた三角形の面積公式 高校数学の美しい物語




Excel 三角形の角度を底辺や斜辺 高さから求める方法 直角三角形の角度の計算




力の分解 三角比編 高校物理をあきらめる前に 高校物理をあきらめる前に




中高生必読 知らないとヤバい二等辺三角形の知識 定義 角度 面積 高校生向け受験応援メディア 受験のミカタ




三角関数の基礎知識




三角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ
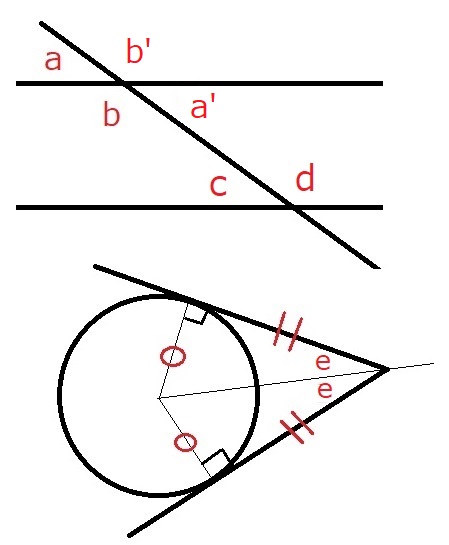



三角関数 機械加工でよく使う計算方法を説明します セドヤのブログ



3




16 合成公式はsinだけじゃないんです 医学生gの数学ノート




三角形のきほんのき 三角関数 中山祐介の土地家屋調査士 測量士補 合格 ブログ
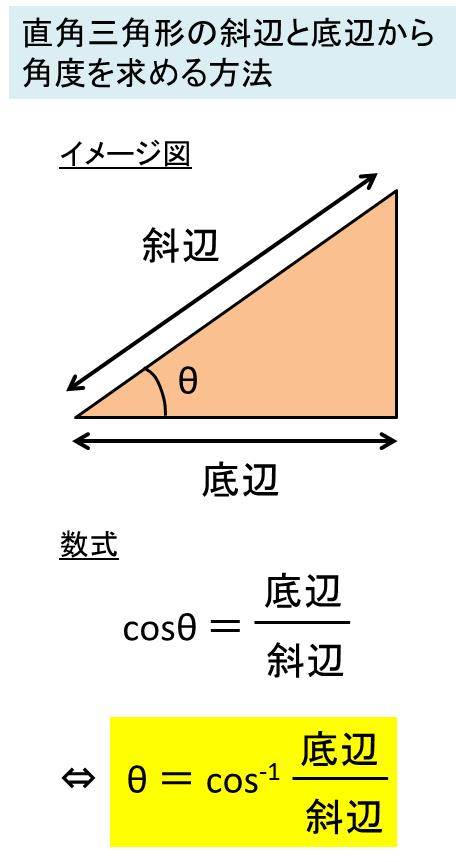



Excel 三角形の角度を底辺や斜辺 高さから求める方法 直角三角形の角度の計算



三角関数の角度の求め方や変換公式 計算問題も徹底解説 受験辞典




Sin Cos Tan 三角比 三角関数の基礎をスタサプ講師がわかりやすく解説 高校生なう スタディサプリ進路 高校生に関するニュースを配信



正確な角度の測定 割り付け




三角関数の知識 やさしい電気回路
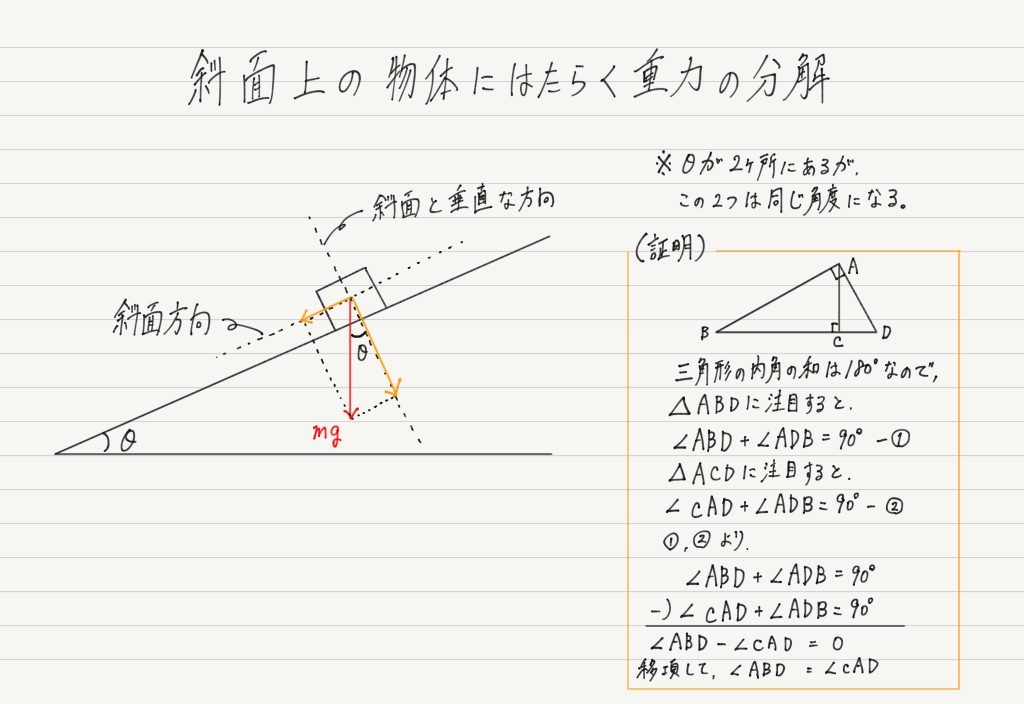



力の分解 三角比編 高校物理をあきらめる前に 高校物理をあきらめる前に



2




正弦定理から 三角形の辺の長さを求める計算について 数学 苦手解決q A 進研ゼミ高校講座
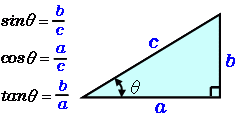



三角関数 度 高精度計算サイト
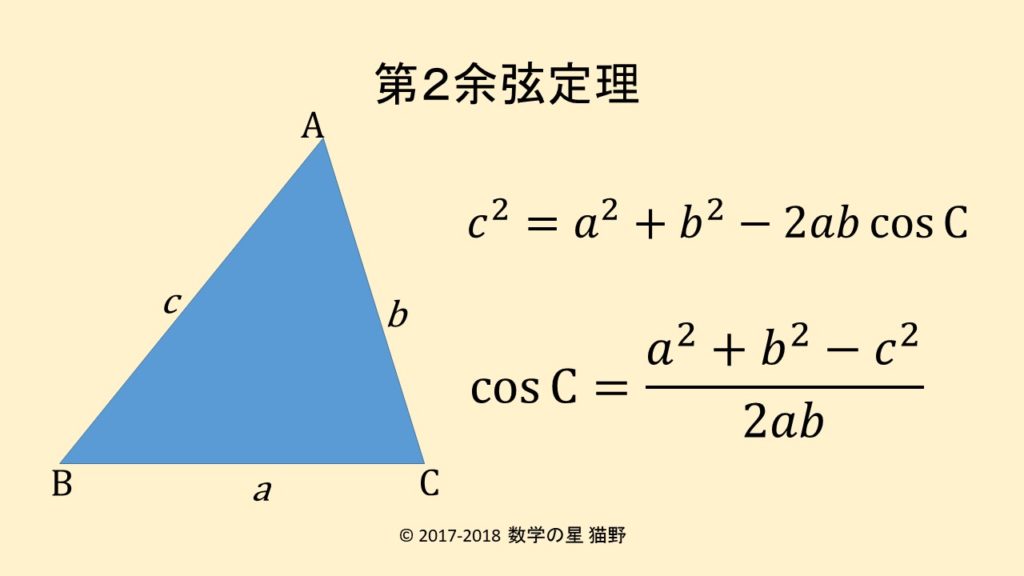



第2余弦定理の公式は辺と角度の関係を簡潔に表す 数学の星




中学数学 正三角形の角度の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



0 件のコメント:
コメントを投稿